
















Ուղղին ուղղահայաց
\(AC\) հատվածը կոչվում է \(A\) կետից \(a\) ուղղին տարված ուղղահայաց, եթե \(AC\) և \(a\) ուղիղները ուղղահայաց են:
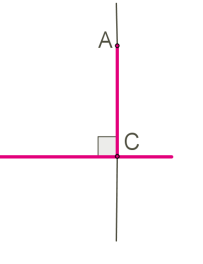
\(C\) կետը կոչվում է ուղղահայացի հիմք:
Ուղղին չպատկանող կետից կարելի է ուղղին տանել ուղղահայաց, ընդ որում՝ միայն մեկը:
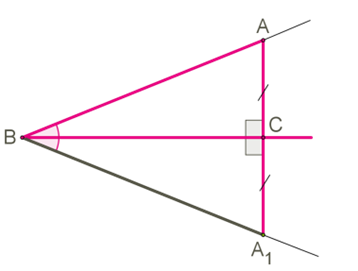
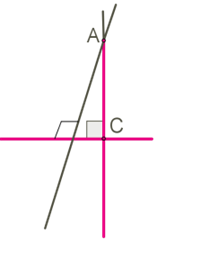
Ապացուցենք, որ \(BC\) ուղղին չպատկանող \(A\) կետից կարելի է տանել ուղղահայաց այդ ուղղին:
Դիցուք, տրված է անկյունը:
\(BC\) ճառագայթի մյուս կողմից տեղադրենք անկյուն, որը հավասար է տրվածին և վերադրենք երկու անկյունները (պատկերացնենք, թե անկյունները թղթի վրա են, և ծալենք թուղթը \(BC\) կողմի երկայնքով):
\(BA\) կողմը կհամընկնի կողմի հետ: Ընդ որում, \(A\) կետը կհամընկնի որևէ կետի հետ:
Հետևաբար, համընկում են և անկյունները:
Բայց և անկյունները կից են, ուրեմն՝ դրանք երկուսն էլ ուղիղ են:
ուղիղը ուղղահայաց է \(BC\) ուղղին, իսկ \(AC\) հատվածը հանդիսանում է ուղղահայաց՝ տարված \(A\) կետից \(BC\) ուղղին:
Եթե ենթադրենք, որ \(A\) կետից կարելի է տանել ևս մեկ ուղղահայաց \(BC\) ուղղին, ապա այն կգտնվի մի ուղղի վրա, որը կհատվի -ի հետ: Բայց, նույն ուղղին ուղղահայաց ուղիղները զուգահեռ են և չեն կարող հատվել:
Այս հակասությունը նշանակում է, որ տրված կետից ուղղին կարելի է տանել միայն մեկ ուղղահայաց:
Եռանկյան միջնագծեր, կիսորդներ և բարձրություններ
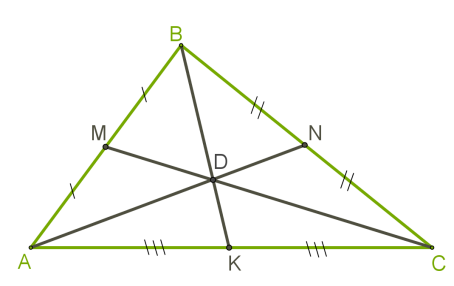
Եռանկյան գագաթը հանդիպակաց կողմի միջնակետի հետ միացնող հատվածը կոչվում է եռանկյան միջնագիծ:
Ուստի միջնագծի կառուցման համար պետք է կատարել հետևյալ գործողությունները:
1. Գտնել կողմի միջնակետը:
2. Միացնել այդ միջնակետը հանդիպակաց գագաթի հետ: Հենց դա կլինի եռանկյան միջնագիծը:
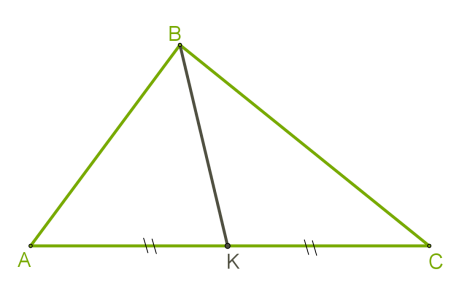
Եռանկյունն ունի երեք կողմ, հետևաբար՝ կարելի է կառուցել երեք միջնագիծ:
Բոլոր միջնագծերը հատվում են նույն կետում:
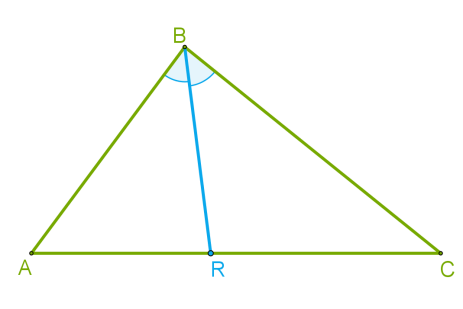
Եռանկյան կիսորդ կոչվում է եռանկյան անկյան կիսորդի վրա գտնվող այն հատվածը, որը միացնում է եռանկյան գագաթը հանդիպակաց կողմի վրա գտնվող կետի հետ:
Ուստի, կիսորդի կառուցման համար պետք է կատարել հետևյալ գործողությունները՝
1. Կառուցել եռանկյան որևէ անկյան կիսորդը (անկյան կիսորդը անկյան գագաթից դուրս եկող ճառագայթ է, որը կիսում է անկյունը):
2. Գտնել անկյան կիսորդի հատման կետը հանդիպակաց կողմի հետ:
3. Միացնել գտնված կետը հանդիպակաց գագաթի հետ: Հենց դա կլինի եռանկյան կիսորդը:
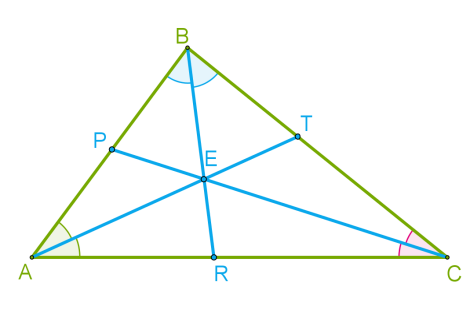
Եռանկյունն ունի երեք անկյուն, հետևաբար՝ կարելի է կառուցել երեք կիսորդ:
Եռանկյան բոլոր կիսորդները հատվում են նույն կետում:
Եռանկյան գագաթից հանդիպակաց կողմը պարունակող ուղղին տարված ուղղահայացը կոչվում է եռանկյան բարձրություն:
Ուստի, բարձրության կառուցման համար պետք է կատարել հետևյալ գործողություները՝
1. Տանել եռանկյան կողմը պարունակող ուղիղը (կարևոր է այն դեպքում, եթե բարձրությունն իջեցնում ենք բութանկյուն եռանկյան սուր անկյունից):
2. Տարված ուղղի հանդիպակաց գագաթից իջեցնենք ուղղահայաց այդ ուղղին (ուղղահայացը եռանկյան գագաթից տարված հատված է, որը կազմում է հանդիպակաց կողմի հետ -ի անկյուն): Հենց դա կլինի եռանկյան բարձրությունը:
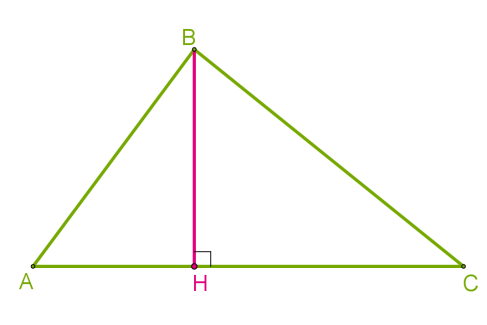
Միջնագծերի և կիսորդների պես եռանկյունն ունի երեք բարձրություն:
Եռանկյան բոլոր բարձրությունները հատվում են նույն կետում:
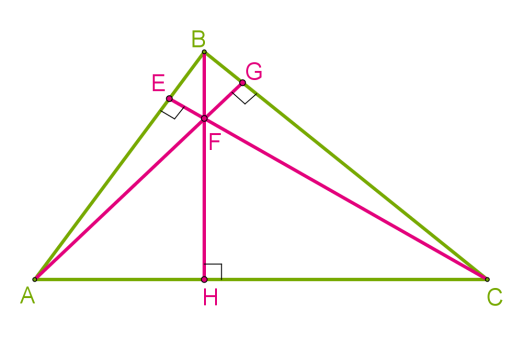
Որոշ եռանկյունների համար բարձրությունների կառուցումը և դրանց հատման կետերի դիրքերը տարբերվում են:
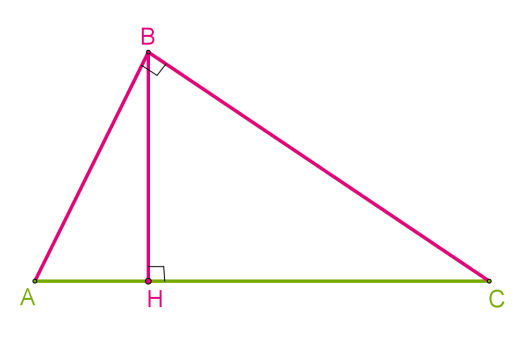
Ուղիղ անկյուն ունեցող եռանկյան մեջ ուղիղ անկյուն առաջացնող կողմերը եռանկյան բարձրություններն են, քանի որ դրանք փոխուղղահայաց են: Այս դեպքում բարձրությունների հատման կետը փոխուղղահայաց կողմերի ընդհանուր գագաթն է:
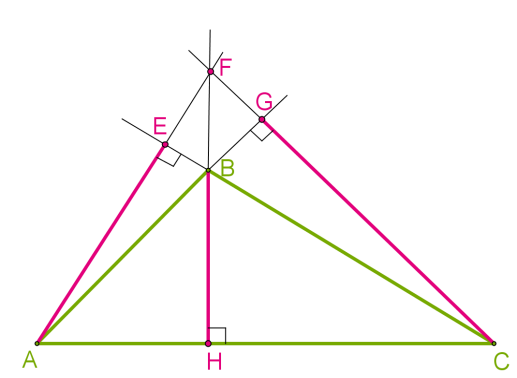
Եթե եռանկյունն ունի բութ անկյուն, ապա սուր անկյուններից իջեցված բարձրությունները դուրս են գալիս եռանկյունից՝ դեպի շարունակված կողմերը: Բարձրությունները պարունակող ուղիղներն այս դեպքում հատվում են եռանկյունից դուրս:
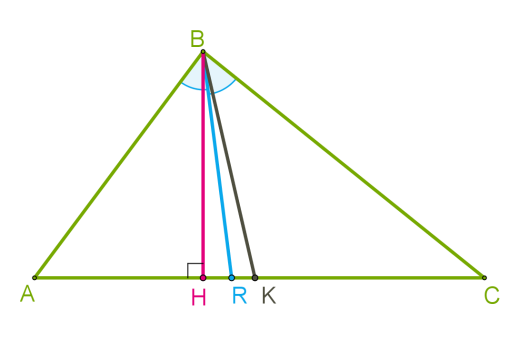
Ուշադրություն
Եթե եռանկյան նույն գագաթից տանենք միջնագիծը, կիսորդը և բարձրությունը, ապա միջնագիծը դրանցից ամենաերկարն է, իսկ բարձրությունը՝ ամենակարճը:
Հավասարասրուն եռանկյուն
Եռանկյունը կոչվում է հավասարասրուն, եթե նրա երկու կողմերը հավասար են: Հավասարասրուն եռանկյան հավասար կողմերը կոչվում են սրունքներ, իսկ երրորդ կողմը՝ հիմք:
\(AB = BC\)՝ սրունքներ, \(AC\)՝ հիմք
Եթե եռանկյան բոլոր երեք կողմերը հավասար են, ապա եռանկյունը կոչվում է հավասարակողմ:
Հավասարասրուն եռանկյունն ունի որոշ հատկություններ, որոնք այլ եռանկյուններ չունեն:
1. Հավասարասրուն եռանկյան հիմքին առընթեր անկյունները հավասար են:
2. Հավասարասրուն եռանկյան հիմքին տարված կիսորդը նաև միջնագիծ է և բարձրություն:
3. Հավասարասրուն եռանկյան հիմքին տարված միջնագիծը նաև կիսորդը է և բարձրություն:
4. Հավասարասրուն եռանկյան հիմքին տարված բարձրությունը նաև կիսորդ է և միջնագիծ:
Առաջին և երկրորդ հատկություններն ապացուցված կլինեն, եթե ապացուցենք, որ հիմքին հանդիպակաց անկյան \(BD\) կիսորդով առաջացած երկու եռանկյունները հավասար են:
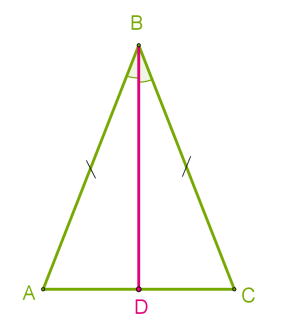
Դիտարկենք \(AC\) հիմքով \(ABC\) հավասարասրուն եռանկյունը և ապացուցենք, որ
Դիցուք \(BD\)-ն \(ABC\) եռանկյան կիսորդն է: Եռանկյունների հավասարության առաջին հայտանիշից եզրակացնում ենք, որ (\(AB = BC\) ըստ պայմանի, \(BD\)-ն ընդհանուր կողմ է, , քանի որ \(BD\)-ն կիսորդ է):
Հավասար եռանկյունների բոլոր համապատասխան մեծությունները հավասար են:
1. ՝ ապացուցված է, որ հիմքին առընթեր անկյունները հավասար են:
2. \(AD = DC\)՝ ապացուցված է, որ կիսորդը նաև միջնագիծ է:
3. ՝ որպես կից անկյուններ, որոնց գումարը հավասար է -ի:
Ուստի, դրանցից յուրաքանչյուրը հավասար է -ի, ինչը նշանակում է, որ միջնագիծը նաև բարձրություն է:
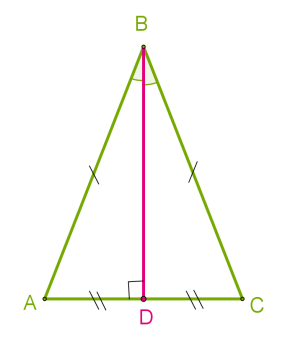
Շատ հեշտ կարելի է ինքնուրույն ապացուցել նաև հավասարասրուն եռանկյունների երրորդ և չորրորդ հատկությունները:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: