
















Ուղղանկյուն եռանկյան հատկությունները
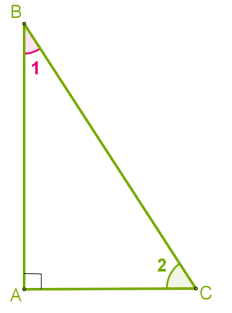
Ուղղանկյուն եռանկյան սուր անկյունների գումարը հավասար է -ի:
Եռանկյան անկյունների գումարը հավասար է -ի, իսկ ուղիղ անկյանը՝ -ի: Հետևաբար, երկու սուր անկյունների գումարը հավասար է՝ \(1 +\)\(2 =\)
Ուղղանկյուն եռանկյան -ի անկյան դիմացի էջը հավասար է ներքնաձիգի կեսին (ներքնաձիգը երկու անգամ մեծ է \(\)\(\)-ի դիմացի էջից):
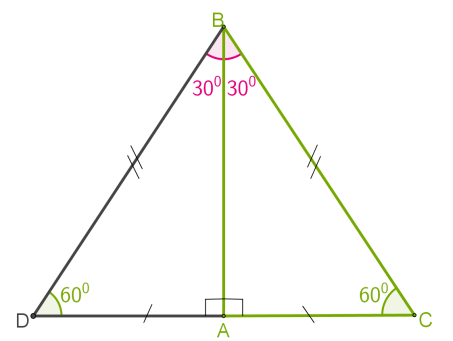
Դիտարկենք \(ABC\) ուղղանկյուն եռանկյունը, որում \(A\)-ն ուղիղ անկյունն է, \(B =\) և ուրեմն՝ \(C =\)
Ապացուցենք, որ \(BC = 2 AC\)
\(ABC\) եռանկյանը կցենք նրան հավասար \(ABD\) եռանկյունը, ինչպես ցույց է տրված վերևի գծագրում:
Ստանում ենք \(BCD\) եռանկյունը, որում \(B =\)\(D =\), ուստի՝ \(DC = BC\): Բայց \(DC = 2 AC\), հետևաբար, \(BC = 2 AC\)
Տեղի ունի նաև հակառակ պնդումը:
Եթե ուղղանկյուն եռանկյան էջը հավասար է ներքնաձիգի կեսին (կամ ներքնաձիգը երկու անգամ մեծ է էջից), ապա այդ էջի դիմացի անկյունը է:
Ուշադրություն
Դեռ Հին Եգիպտոսում հայտնի էր.
եթե եռանկյան կողմերը համապատասխանաբար հավասար են \(3, 4\) և \(5\) միավորի, ապա այդ եռանկյունը ուղղանկյուն է և նրա ներքնաձիգը \(5\) է:
Նույն պնդումը ճիշտ է, եթե եռանկյան կողմերը նշված թվերի բազմապատիկներն են:
Նույն պնդումը ճիշտ է, եթե եռանկյան կողմերը նշված թվերի բազմապատիկներն են:
Ասածից հետևում է նաև հակառակ պնդումը.
եթե ուղղանկյուն եռանկյան էջերը հավասար են \(3\) և \(4\) միավորի, ապա նրա ներքնաձիգը հավասար է \(5\)-ի: Այս դեպքում նույնպես պնդումը ճիշտ է, երբ եռանկյան կողմերը նշված թվերի բազմապատիկներն են:
Ուղղանկյուն եռանկյունների հավասարության հայտանիշները
1. Եթե մի ուղղանկյուն եռանկյան էջերը հավասար են մյուս ուղղանկյուն եռանկյան էջերին, ապա այդ եռանկյունները հավասար են:
2. Եթե ուղղանկյուն եռանկյան էջը և նրան առընթեր անկյունը հավասար են համապատասխանաբար մյուս ուղղանկյուն եռանկյան էջին և նրան առընթեր անկյանը, ապա եռանկյունները հավասար են:
3. Եթե մի ուղղանկյուն եռանկյան ներքնաձիգն ու սուր անկյունը համապատասխանաբար հավասար են մյուս ուղղանկյուն եռանկյան ներքնաձիգին և սուր անկյանը, ապա եռանկյունները հավասար են:
4. Եթե մի ուղղանկյուն եռանկյան ներքնաձիգն ու էջը համապատասխանաբար հավասար են մյուս ուղղանկյուն եռանկյան ներքնաձիգին և էջին, ապա եռանկյունները հավասար են:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: