
















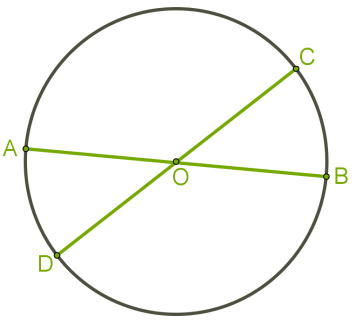
Տրված է \(O\) կենտրոնով շրջանագիծ և նրա երկու տրամագծերը՝ \(AB\) -ն և \(CD\) -ն:
Որոշիր \(AOD\) եռանկյան պարագիծը, եթե \(CB\)\(=\)8 սմ, \(AB\)\(=\)34 սմ:
1. Ձևակերպիր շրջանագծի շառավղի հատկությունը՝
շրջանագծի բոլոր շառավիղներն ունեն :
2. Նշիր \(AOD\) եռանկյանը հավասար եռանկյունը՝ \(AOD\)\(=\) :
3. սմ: