
















Անկյան կիսորդի հատկությունը
Թեորեմ: Անկյան կիսորդի ցանկացած կետ հավասարահեռ է այդ անկյան կողմերից:
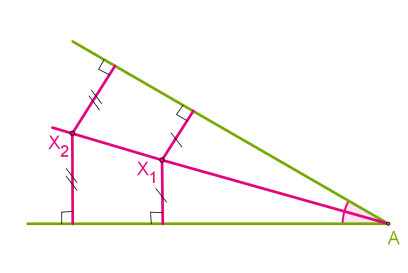
Ապացուցենք այս թեորեմը: Նայիր վերևի նկարին:
Կիսորդով առաջացած եռանկյունների անկյունները համապատասխանաբար հավասար են: Իրոք, մի զույգի անկյունները հավասար են՝ ըստ կիսորդի սահմանման, մյուս զույգի անկյունները \(90\) աստիճան են (կետի հեռավորությունները ուղիղներից): Հետևաբար, հավասար է նաև երրորդ զույգի անկյունները (անկյունների գումարը պետք է \(180°\) լինի):
Քանի որ դիտարկվող ուղղանկյուն եռանկյունների ներքնաձիգը ընդհանուր է (կիսորդի վրա գտնվող կողմը), ապա եռանկյունները հավասար են` ըստ եռանկյունների հավասարության երկրորդ հայտանիշի (կողմ և առընթեր երկու անկյուններ): Հետևաբար, հավասար են նաև համապատասխան էջերը:
Հատվածի միջնուղղահայացի հատկությունը
Հատվածին ուղղահայաց և նրա միջնակետով անցնող ուղիղը կոչվում է հատվածի միջնուղղահայաց:
Թեորեմ: Միջնուղղահայացի ցանկացած կետ հավասարահեռ է այդ հատվածի ծայրակետերից:
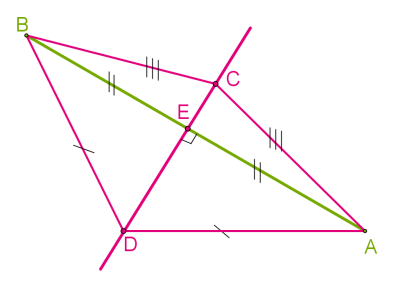
Պետք է ապացուցել, որ \(AC\) և \(BC\) հատվածները հավասար են: Դրանում կարելի է համոզվել, եթե ապացուցեք, որ հավասար են \(BEC\) և \(AEC\) ուղղանկյուն եռանկյունները:
Ըստ միջնուղղահայացի սահմանման՝ \(E\) անկյունը ուղիղ է և \(AE = BE\): Քանի որ \(CE\)-ն ընդհանուր կողմ է, ապա դիտարկվող եռանկյունները հավասար են՝ ըստ եռանկյունների հավասարության առաջին հայտանիշի (երկու կողմեր և դրանցով կազմված անկյուններ):
Հետևաբար, հավասար են նաև եռանկյունների ներքնաձիգները:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի. Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: