
















Եռանկյան անկյունների գումարը
Եռանկյան անկյունների գումարը \(180°\) է:
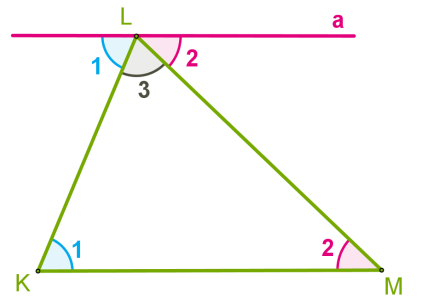
Ապացույց:
Դիտարկենք \(KLM\) կամայական եռանկյունը և ապացուցենք, որ \(K +\)\(L +\)\(M =\)
\(L\) գագաթով տանենք \(KM\) կողմին զուգահեռ \(a\) ուղիղը: \(1\)-ով նշանակված անկյունները խաչադիր են՝ առաջացել են \(a\) և \(KM\) զուգահեռ ուղիղները \(KL\)-ով հատելիս:
\(2\)-ով նշանակված անկյունները ևս խաչադիր են և առաջացել են նույն զուգահեռ ուղիղները \(ML\)-ով հատելիս:
Ակնհայտ է, որ \(1\), \(2\) և \(3\) անկյունների գումարը հավասար է \(L\) գագաթով փռված անկյանը, հետևաբար՝
\(1 +\)\(2 +\)\(3 =\) կամ \(K +\)\(L +\)\(M =\):
Թեորեմն ապացուցված է:
Եռանկյան անկյունների գումարի մասին թեորեմի հետևանքները
Հետևանք 1. Ուղղանկյուն եռանկյան սուր անկյունների գումարը է:
Հետևանք 2. Հավասարասրուն ուղղանկյուն եռանկյան յուրաքանչյուր սուր անկյուն հավասար է -ի:
Հետևանք 3. Հավասարակողմ եռանկյան բոլոր երեք անկյունները հավասար են -ի:
Հետևանք 4. Ցանկացած եռանկյան մեջ կամ բոլոր անկյունները սուր են, կամ անկյուններից երկուսը սուր են, իսկ երրորդը՝ բութ կամ ուղիղ:
Հետևանք 5. Եռանկյան արտաքին անկյունը հավասար է երկու ներքին անկյունների գումարին, որոնք կից չեն արտաքին անկյանը:
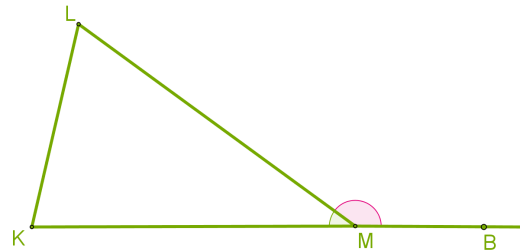
Ապացույց:
\(KML +\)\(BML =\) և \(K +\)\(L +\)\(KML =\) հավասարություններից ստանում ենք, որ \(BML =\)\(K +\)\(L\)
Սուրանկյուն, ուղղանկյուն և բութանկյուն եռանկյուններ
Եռանկյան անկյունների գումարի թեորեմի չորրորդ հետևանքի համաձայն՝ անկյուններից կախված գոյություն ունեն եռանկյունների երեք տեսակներ:
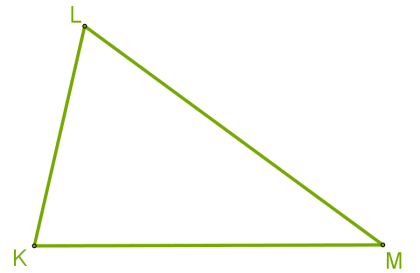
\(KLM\) եռանկյան բոլոր անկյունները սուր են:
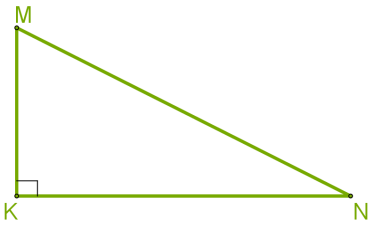
\(KLM\) եռանկյան անկյուններից մեկն ուղիղ է՝ \(K = 90\)
Ուղղանկյուն եռանկյան ուղիղ անկյան դիմացի կողմը կոչվում է ներքնաձիգ, իսկ մյուս երկու կողմերը՝ էջեր:
Վերևի նկարում \(LN\)-ը ներքնաձիգն է, իսկ \(LK\)-ն և \(KN\)-ը՝ էջերը:
\(KLM\) եռանկյան անկյուններից մեկը բութ է:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: