
















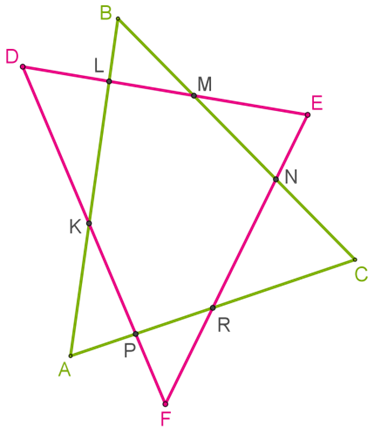
\(ABC\) եռանկյան պարագիծը 5 սմ է, իսկ \(DEF\) եռանկյան պարագիծը՝ 7 սմ է:
Ապացուցիր, որ \(PKLMNR\) վեցանկյան պարագիծը փոքր է 6 սմ-ից:
1. Դիտարկիր \(PAK\), \(KDL\), \(LBM\), \(MEN\), \(NCR\) և \(RFP\) եռանկյունները, և գրիր դրանցից յուրաքանչյուրի համար եռանկյան անհավասարությունը, այն կողմերի համար, որոնք նաև վեցանկյան կողմերն են՝
\(PK\) \(<\) \(PA\) \(+\)
\(KL\)\(<\)\(+\)
\(<\)\(+\)
\(<\)\(+\)
\(<\)\(+\)
\(<\)\(+\)
2. Եթե գումարենք ճիշտ անհավասարությունների ձախ և աջ մասերը, ապա կստացվի ճիշտ անհավասարություն:
Առաջադրանքի ո՞ր մեծությունը ստացվեց ձախ մասում գումարելուց հետո:
3. Եթե ճիշտ անհավասարության երկու մասերին գումարենք նույն մեծությունը, ապա կստացվի ճիշտ անհավասարություն:
Նախորդ քայլում ստացված ճիշտ անհավասարության երկու մասերին գումարիր \(PK + KL + LM + MN + NR + RP\) մեծությունը:
Առաջադրանքի ո՞ր մեծությունը ստացվեց ձախ մասում գումարելուց հետո:
4. Առաջադրանքի ո՞ր մեծությունները ստացվեցին աջ մասում, գումարելուց հետո:
5. Ինչի՞ հավասար կլինի ստացված անհավասարության աջ մասը, եթե տեղադրենք առաջադրանքի թվային տվյալները:
Պատասխան՝ :
6. Ի՞նչ պետք է անել ստացված անհավասարության երկու կողմերի հետ ապացուցելու համար, որ \(PKLMNR\) վեցանկյան պարագիծը փոքր է 6 սմ-ից: