
















Առնչություններ եռանկյան կողմերի և անկյունների միջև
Եռանկյան ավելի մեծ կողմի դիմաց ընկած է ավելի մեծ անկյունը:
Ապացույց:
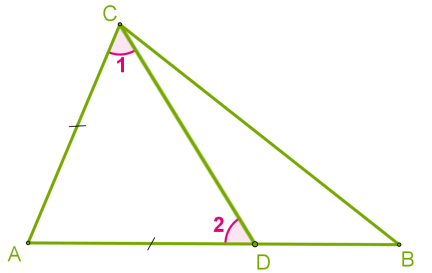
Դիցուք \(ABC\) եռանկյան մեջ \(AB\) կողմն ավելի մեծ է \(AC\) կողմից:
Ապացուցենք, որ \(C >\)\(B\):
Տեղադրենք \(AB\) կողմի վրա \(AC\)-ին հավասար հատված:
Քանի որ \(AD < AB\), ապա \(D\) կետն ընկած է \(A\) և \(B\) կետերի միջև:
Հետևաբար, \(1\) անկյունը հանդիսանում է \(C\) անկյան մաս, և ուրեմն՝ \(C >\)\(1\)
\(2\) անկյունը \(BDC\) եռանկյան արտաքին անկյունն է, ուստի \(2 >\)\(B\)
\(1 =\) \(2\)՝ որպես \(ADC\) հավասարասրուն եռանկյան հիմքին առընթեր անկյուններ:
Այսպիսով, \(C >\)\(1 =\)\(2 >\)\(B\)
Այստեղից հետևում է, որ \(C >\)\(B\)
Տեղի ունի նաև հակառակ պնդումը.
Եռանկյան ավելի մեծ անկյան դիմաց ընկած է ավելի մեծ կողմ:
Հետևանքներ.
Հետևանք 1.
Եթե եռանկյան երկու անկյուններ հավասար են, ապա եռանկյունը հավասարասրուն է (հավասարասրուն եռանկյան հայտանիշ):
Հետևանք 2.
Եթե եռանկյան երեք անկյուններ հավասար են, ապա եռանկյունը հավասարակողմ է:
Հետևանք 3.
Ուղղանկյան եռանկյան ներքնաձիգն ավելի մեծ է էջից:
Եռանկյան անհավասարությունը
Եռանկյան յուրաքանչյուր կողմ ավելի փոքր է, քան մյուս երկու կողմերի գումարը:
Ապացույց:
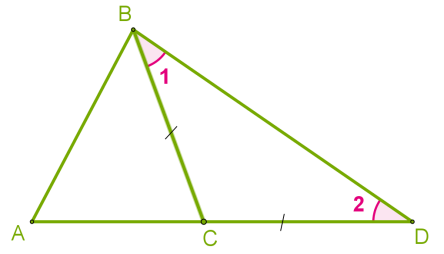
Դիտարկենք \(ABC\) եռանկյունը և ապացուցենք, որ \(AB < AC + BC\)
Շարունակենք \(AC\) կողմը և տեղադրենք հատված \(CD = BC\)
\(BCD\) եռանկյունը հավասարասրուն է, հետևաբար \(1 = \)\(2\)
\(ABD\) եռանկյան մեջ, ակնհայտորեն \(ABD >\)\(1\), ինչը նշանակում է, որ \(ABD >\)\(2\)
Քանի որ ավելի մեծ անկյան դիմաց ընկած է ավելի մեծ կողմ, ապա \(AB < AD\), և \(AD =
AC + BC\):
Հետևաբար, \(AB < AC + BC\)
Հետևանք 4.
Մի ուղղի վրա չգտնվող \(A, B\) և \(C\) կետերի համար տեղի ունեն հետևյալ անհավասարությունները՝
\(AB < AC + CB, AC < AB + BC, BC < AB + AC\)
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: