
















Ուղղի և հարթության փոխդասավորությունը
Պարզենք, թե տարածության մեջ ի՞նչ փոխդասավորություն կարող են ունենալ ուղիղն ու հարթությունը:
Առաջին դեպք: Գիտենք, որ եթե ուղղի երկու կետեր ընկած են հարթության մեջ, ապա ուղիղը ամբողջությամբ ընկած է այդ հարթության մեջ: Սա ուղղի և հարթության փոխդասավորության դեպքերից մեկն է (տես ներքևի նկարը):
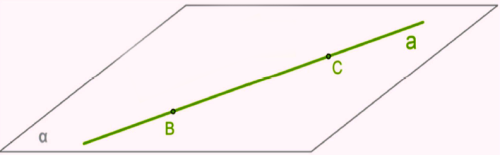
Երկրորդ դեպք: Գիտենք նաև ուղղի և հարթության փոխդասավորության ևս մեկ դեպք՝ երբ ուղիղն ու հարթությունը ունեն մեկ ընդհանուր կետ:
Այդպես է ստացվում, եթե հարթության որևէ կետով և հարթությունից դուրս գտնվող կետով տարվում է ուղիղ (տես ներքևի նկարը):
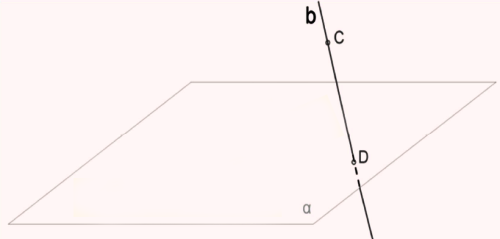
Երրորդ դեպք: Հնարավոր է ուղղի և հարթության փոխդասավորության վերջին դեպքը՝ երբ ուղիղն ու հարթությունը չեն հատվում (տես ներքևի նկարը):
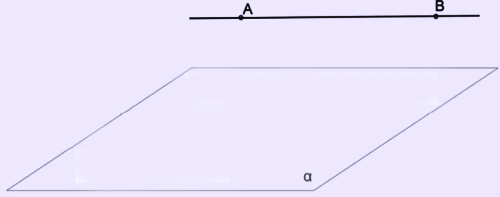
Այս վերջին դեպքում ուղիղն ու հարթությունը կոչվում են զուգահեռ:
Ուղիղը և հարթությունը կոչվում են զուգահեռ, եթե նրանք ընդհանուր կետ չունեն:
Թեորեմ: Եթե ուղիղը զուգահեռ է հարթությանը և ընկած է այդ հարթությունը հատող մեկ այլ հարթության մեջ, ապա այն զուգահեռ է նաև երկու հարթությունների հատման գծին:
Ապացույց:
Դիցուք \(a\) ուղիղը զուգահեռ է \(α\) հարթությանը, \(ß\)-ն երկրորդ հարթությունն է, և \(b\)-ն երկու հարթությունների հատման գիծն է: Համոզվենք, որ \(a\) և \(b\) ուղիղները զուգահեռ են: Իրոք, \(a\) և \(b\) ուղիղները ընկած են \(ß\) հարթության մեջ: Եթե նրանք զուգահեռ չլինեն, ապա կունենան ընդհանուր կետ, որը կպատկանի նաև \(α\) հարթությանը: Այդ դեպքում \(a\) ուղիղն ու \(α\) հարթությունը ևս կունենան ընդհանուր կետ, և հետևաբար, զուգահեռ լինել չեն կարող:
Ստացած հակասությունը ապացուցում է թեորեմի պնդումը:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009