
















Երկու ուղիղների և հարթության փոխդասավորությունը
Դիտարկենք տարածության մեջ երկու ուղիղների և հարթության փոխդասավորության դեպքերը:
Առաջին դեպք: Դիցուք երկու ուղիղները զուգահեռ են, և հայտնի է, որ նրանցից մեկը ընկած է հարթության մեջ, իսկ մյուսը՝ ոչ: Պարզենք, թե ինչպե՞ս են դասավորված երկրորդ ուղիղն ու հարթությունը:
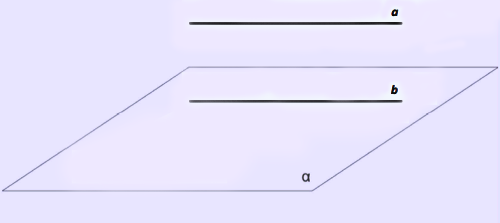
Թեորեմ 1: Եթե տրված հարթության մեջ չգտնվող ուղիղը զուգահեռ է այդ հարթության մեջ գտնվող որևէ ուղղի, ապա այն զուգահեռ է նաև տրված հարթությանը:
Ապացույց:
Դիցուք \(b\) ուղիղը զուգահեռ է \(a\) ուղղին և ընկած է \(α\) հարթության մեջ, իսկ \(a\)-ն ընկած չէ \(α\) հարթության մեջ: Համոզվենք, որ \(a\)-ն զուգահեռ է \(α\) հարթությանը:
Դիտարկենք \(a\) և \(b\) զուգահեռ ուղիղներով անցնող \(ß\) հարթությունը:
\(α\) և \(ß\) հարթությունները չեն համընկնում և ունեն ընդհանուր ուղիղ՝ \(b\)-ն:
Եթե \(a\)-ն հատեր \(α\) հարթությունը, ապա հատման կետը ընկած կլիներ \(α\) և \(ß\) հարթությունների ընդհանուր ուղղի՝ \(b\)-ի վրա:
Դա հնարավոր չէ, քանի որ \(a\) և \(b\) ուղիղները զուգահեռ են:
Ստացած հակասությունը ապացուցում է թեորեմի պնդումը:
Երկրորդ դեպք: Դիցուք երկու ուղիղները զուգահեռ են, և հայտնի է, որ նրանցից մեկը հատում է տրված հարթությունը: Պարզենք, թե ինչպե՞ս են դասավորված երկրորդ ուղիղն ու հարթությունը:
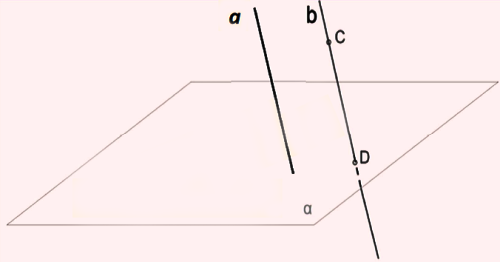
Թեորեմ 2: Եթե երկու զուգահեռ ուղիղներից մեկը հատում է որևէ հարթություն, ապա մյուսը ևս հատում է այդ հարթությունը:
Ինքնուրույն համոզվիր, որ \(b\)-ն ևս հատում է \(α\) հարթությունը:
Ցուցում: Համոզվիր, որ մնացած դեպքերը հնարավոր չեն (բերում են հակասության):
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009