
















Երեք հարթությունների վերաբերյալ թեորեմներ
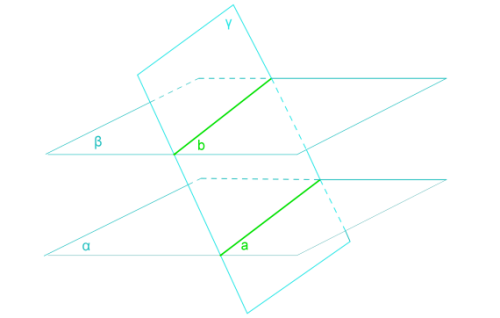
Թեորեմ 1. Երկու զուգահեռ հարթությունները երրորդ հարթությամբ հատելուց ստացված ուղիղները զուգահեռ են:
Ապացույց:
Դիցուք -ն և -ն զուգահեռ հարթություններ են, հարթությունները հատում են դրանք:
\(a\) ուղիղը և հարթություների հատման գիծն է:
\(b\) ուղիղը և հարթություների հատման գիծն է:
\(a\) և \(b\) ուղիղները գտնվում են միևնույն հարթության մեջ, ուստի, դրանք կամ հատվող են, կամ էլ՝ զուգահեռ են: Քանի որ դրանք ընկած են երկու զուգահեռ հարթություններում, ապա դրանք ընդհանուր կետեր ունենալ չեն կարող:
Այսպիսով, \(a\) և \(b\) ուղիղները զուգահեռ են:
Թեորեմն ապացուցված է:
Թեորեմ 2. Զուգահեռ ուղիղների այն հատվածները, որոնց ծայրակետերն ընկած են երկու զուգահեռ հարթությունների մեջ, հավասար են:
Ապացույց:
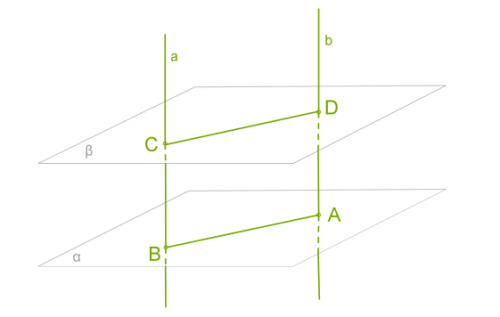
Դիցուք -ն և -ն զուգահեռ հարթություններ են, \(a\) և \(b\) զուգահեռ ուղիղները հատում են դրանք:
Քանի որ \(a\) և \(b\) ուղիղները զուգահեռ են, ապա դրանցով անցնում է միակ հարթությունը:
Այդ հարթությունը հարթությունը հատում է \(AB\) ուղղով, իսկ հարթությունը՝ \(CD\) ուղղով:
Ըստ նախորդ թեորեմի \(AB\) և \(CD\) ուղիղները զուգահեռ են:
Առաջացած \(ABCD\) քառանկյունը զուգահեռագիծ է (նրա հանդիպակաց կողմերը զուգահեռ են): Զուգահեռագծի հանդիպակաց կողմերը հավասար են, ուստի, \(BC = AD\)
Թեորեմն ապացուցված է:
Ինքնուրույն համոզվիր, որ տեղի ունեն հետևյալ երկու պնդումները:
Միևնույն հարթությանը զուգահեռ երկու հարթությունները զուգահեռ են:
Հարթությունից դուրս գտնվող կետով անցնում է այդ հարթությանը զուգահեռ մեկ հարթություն:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009: