Զուգահեռ հարթությունների հեռավորությունը

Մենք արդեն գիտենք որոշել կետի հեռավորությունը ուղղից կամ հարթությունից: Դրա համար այդ կետից տրված ուղղին կամ հարթությանը իջեցվում է ուղղահայաց:

Նույն կերպ վարվում ենք նաև զուգահեռ հարթությունների կամ զուգահեռ ուղղի և հարթության հեռավորությունը որոշելիս:

Երկու զուգահեռ հարթություններից մեկի բոլոր կետերը հավասարահեռ են մյուս հարթությունից:

Հետևաբար, երկու հարթությունների միջև հեռավորությունը կարելի է սահմանել հետևյալ կերպ:

Երկու զուգահեռ հարթությունների հեռավորություն կոչվում է հարթություններից մեկի կամայական կետի հեռավորությունը մյուս հարթությունից:

Դիցուք տրված են

α

β

զուգահեռ հարթությունները՝

α ∥ β

Դրանց միջև հեռավորությունը հաշվելու համար պետք է՝

- հարթություններից մեկի, օրինակ՝

α

-ի վրա վերցնել կամայական կետ, օրինակ՝ \(A\)-ն,

- այդ կետից իջեցնել ուղղահայաց

β

հարթության վրա:

Այդ ուղղահայացի երկարությունը հենց կլինի

α

β

հարթությունների հեռավորությունը:

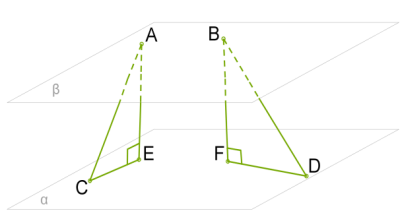
Այսպիսով, ներքևի նկարում

α

β

զուգահեռ հարթությունների հեռավորությունը \(AE = BF\) երկարությունն է:

Նույն ձևով սահմանում ենք ուղղի և նրան զուգահեռ հարթության հեռավորությունը:

Հարթությանը զուգահեռ ուղղի բոլոր կետերը հավասարահեռ են այդ հարթությունից:

Հետևաբար, ուղղի և նրան զուգահեռ հարթության հեռավորությունը սահմանում ենք այսպես:

Ուղղի և նրան զուգահեռ հարթության հեռավորություն կոչվում է ուղղի կամայական կետի հեռավորությունը այդ հարթությունից:

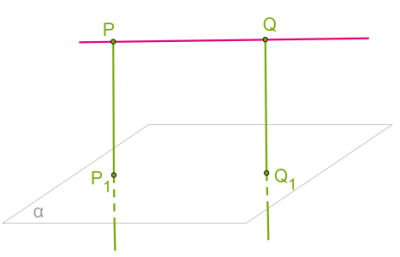
Ներքևի նկարում \(PQ\) ուղղի և նրան զուգահեռ

α

հարթության հեռավորությունը

P P_{1} = Q Q_{1}

երկարությունն է:

Աղբյուրները

Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009:

Սխա՞լ ես գտել

1. Զուգահեռ հարթությունների հեռավորությունը