
















Ուղղահայաց ուղիղներ տարածության մեջ
Երկու ուղիղներ կոչվում են ուղղահայաց, եթե նրանց կազմած անկյունը \(90°\)է:
Հարթության մեջ ուղղահայաց են միայն հատվող ուղիղները: Տարածության մեջ պատկերը այլ է՝ ուղղահայաց կարող են լինել նաև խաչվող ուղիղները:
Հիշենք, որ խաչվող ուղիղների կազմած անկյունը հաշվելու համար պետք է դրանք տեղադրել նույն հարթության մեջ:
Ինչպես և հարթության մեջ, \(a\) և \(b\) ուղիղների ուղղահայացությունը նշանակում են այսպես՝ :
Եթե երկու զուգահեռ ուղիղներից մեկը ուղղահայաց է երրորդ ուղղին, ապա մյուսը ևս ուղղահայաց է այդ ուղղին:
Հրթության մեջ ուղղին պատկանող կետից կարելի է տանել այդ ուղղին ուղղահայաց միակ ուղիղը:
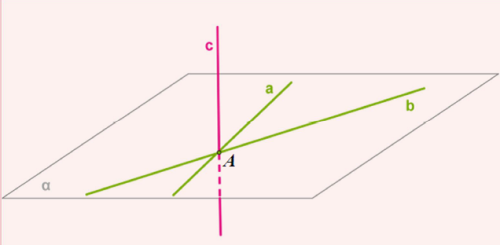
Վերևի նկարից երևում է, որ \(A\) կետից \(c\) ուղղի տարված են երկու ուղիղներ՝ \(a\)-ն և \(b\)-ն: Ավելին, դժվար չէ պատկերացնել, որ \(α\) հարթության մեջ \(A\) կետով անցնող ցանկացած ուղիղ ուղղահայաց կլինի \(c\) ուղղին: Ստացվում է, որ
Տրված ուղղին պատկանող կետով կարելի է տանել նրան ուղղահայաց անվերջ թվով ուղիղներ:
Հաջորդ թեմայում կտեսնենք, որ այդ բոլոր ուղիղները գտնվում են միևնույն հարթության մեջ:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009