
















Խնդիրների լուծման ժամանակ կարևոր է պարզել անկյունագծերի և կողմնային նիստերի կազմած անկյունները:
Թեքի և հարթության կազմած անկյունը թեքի և այդ հարթության վրա նրա պրոյեկցիայի կազմած անկյունն է:
Թեքի և հարության կազմած անկյունը գտնելու համար պետք է կատարել հետևյալ քայլերը.
1. տանել թեքը,
2. թեքի խայրակետից իջեցնել ուղղահայաց հարթության վրա,
3. տանել թեքի պրոյեկցիան,
4. նշել թեքի և նրա պրոյեկցիայի կազմած անկյունը:
Ուղղանկյունանիստի անկյունագծի և հիմքի հարթության կազմած անկյունը
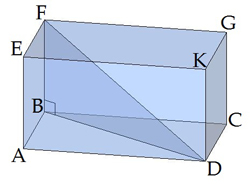
\(DF\) անկյունագծի և հիմքի \(ABCD\) հարթության կազմած անկյունը \(BDF\) անկյունն է: \(DBF\)-ը ուղղանկյուն եռանկյուն է:
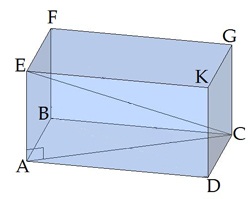
\(EC\) անկյունագծի և հիմքի \(ABCD\) հարթության կազմած անկյունը \(ECA\) անկյունն է: \(ECA\)-ը ուղղանկյուն եռանկյուն է:
Ուղղանկյունանիստի անկյունագծի և կողմնային նիստի կազմած անկյունը
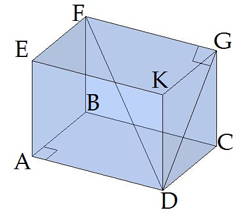
\(FD\) անկյունագծի և հիմքի \(DKGC\) կողմնային նիստի կազմած անկյունը \(FDG\) անկյունն է:
Ուշադրություն
Ուղղանկյունանիստի կողը ուղղահայաց է նրա կողմնային նիստի, հոտևաբար, \(DFG\)-ն ուղղանկյուն եռանկյուն է:
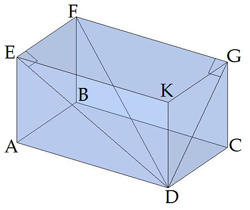
\(FD\) անկյունագծի և հիմքի \(AEKD\) կողմնային նիստի կազմած անկյունը \(FDE\) անկյունն է:
Ուշադրություն
Ուղղանկյունանիստի կողը ուղղահայաց է նրա կողմնային նիստի, հոտևաբար, \(FDE\)-ն ուղղանկյուն եռանկյուն է:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009