
















Կետի հեռավորությունը հարթությունից
Հիշենք սահմանումները:
Հարթությունից դուրս վերցված կետից հարթությանը տարված թեք կոչվում է այդ կետը հարթության որևէ կետի հետ միացնող ցանկացած հատված, որը ուղղահայաց չէ հարթությանը:
Հարթությունից դուրս վերցված կետից հարթությանը տարված ուղղահայաց կոչվում է այդ կետը հարթության կետի հետ միացնող այն հատվածը, որը ուղղահայաց է հարթությանը:
Թեքի և հարթության կազմած անկյուն կոչվում է թեքի և նրա պրոյեկցիայի կազմած անկյունը:
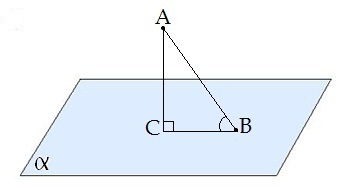
\(AB\)-ն թեք է:
\(AC\)-ն ուղղահայաց է:
\(B\)-ն թեքի հիմքն է:
\(C\)-ն ուղղահայացի հիմքն է:
\(CB\)-ն \(AB\) թեքի պրոյեկցիան է հարթության վրա:
\(CBA\)-ն \(AB\) թեքի և հարթության կազմած անկյունն է:
Դիցուք \(A\) կետը վերցված է հարթությունից դուրս:
\(A\) կետից հարթությանն իջեցված ուղղահայացը միակն է:
\(A\) կետից հարթությանն իջեցված ուղղահայացը փոքր է նույն կետից տարված ցանկացած թեքից:
Եթե \(AB\)-ն \(A\) կետից հարթությանը տարված թեքերից ամենափոքրն է, ապա հենց \(AB\)-ն է \(A\) կետից հարթությանն իջեցված ուղղահայացը:
Կետի հեռավորություն հարթությունից կոչվում է այդ կետից հարթությանն իջեցված ուղղահայացի երկարությունը:
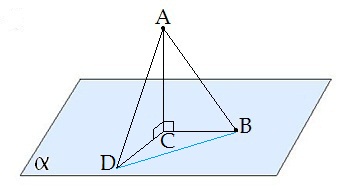
Եթե \(AD > AB\), ապա \(DC > BC\)
Եթե տրված կետից հարթությանը տարված են մի քանի թեքեր, ապա ավելի մեծ թեքն ունի ավելի մեծ պրոյեկցիա այդ հարթության վրա:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009