
















Ուղղի և հարթության ուղղահայացությունը
Հարթությունը հատող ուղիղը կոչվում է ուղղահայաց հարթությանը, եթե այն ուղղահայաց է այդ հարթության մեջ ընկած ցանկացած ուղղի:
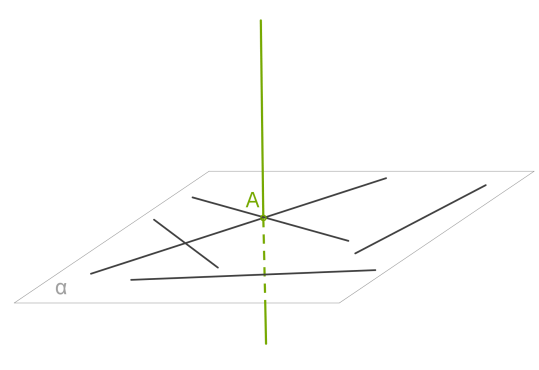
Ուղղի և հարթության ուղղահայացությունը նշանակում են այսպես՝ :
Տարածության ցանկացած կետով անցնում է տրված հարթությանը ուղղահայաց միակ ուղիղը:
Ուղղի և հարթության ուղղահայացության հայտանիշը:
Եթե ուղիղը ուղղահայաց է հարթության մեջ ընկած երկու հատվող ուղիղների, ապա այն ուղղահայաց է հարթությանը:
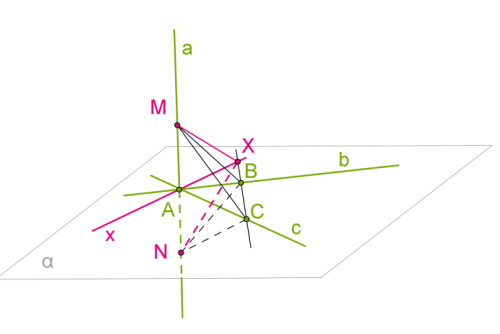
Դիցուք \(a\) ուղիղը ուղղահայց է \(α\) հարթության մեջ ընկած \(b\) և \(c\) ուղիղներին:
\(a\) ուղիղը տանենք \(b\) և \(c\) ուղիղների հատման \(A\) կետով և ապացուցենք, որ այն ուղղահայաց է \(α\) հարթության մեջ ընկած ցանկացած ուղղի:
1. Դիցուք \(x\)-ը \(A\) կետով անցնող ցանկացած ուղիղ է \(α\) հարթության մեջ: Ցույց տանք, որ այն ուղղահայաց է \(a\) ուղղին:
\(α\) հարթության մեջ տանենք \(A\) կետով չանցնող որևէ ուղիղ, որը հատում է \(b\), \(c\) և \(x\) ուղիղները: Հատման կետերը նշանակենք \(B\), \(C\) և \(X\):
2. \(a\) ուղղի վրա \(A\) կետից երկու ուղղություններով տեղադրենք \(AM\) և \(AN\) հավասար հատվածները:
3. \(MCN\) եռանկյունը հավասարասրուն է, քանի որ ըստ թեորեմի պայմանի \(AC\)-ն նրա բարձրությունն է և ըստ կառուցման նաև նրա միջնագիծն է (\(AM=AN\)):
Նույն պատճառով հավասարասրուն է նաև \(MBN\) եռանկյունը:
4. Հետևաբար, \(MBC\) և \(NBC\) եռանկյունները հավասար են՝ ըստ երեք կողմերի:
5. \(MBC\) և \(NBC\) եռանկյունների հավասարությունից հետևում է, որ հավասար են \(MBX\) և \(NBX\) անկյունները, և հետևաբար, նաև \(MBX\) և \(NBX\) եռանկյունները ըստ երկու կողմերի և նրանց կազմած անկյան:
6. Այդ եռանկյունների \(MX\) և \(NX\) կողմերի հավասարությունից եզրակացնում ենք, որ \(MXN\) եռանկյունը հավասարասրուն է: Ուստի նրա \(XA\) միջնագիծը նաև բարձրություն է:
Սա նշանակում է, որ \(x\) և \(a\) ուղիղները ուղղահայաց են:
Այսպիսով, ըստ սահմանման \(a\) ուղիղը ուղղահայաց է \(α\) հարթությանը:
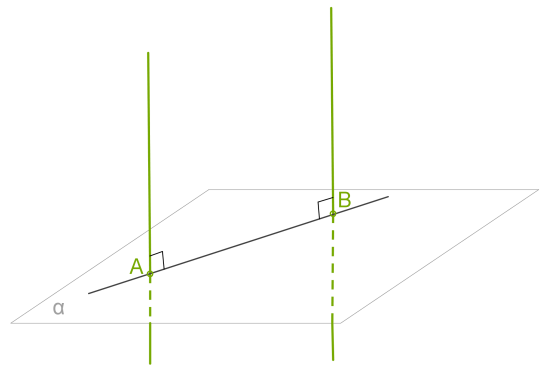
1. Եթե հարթությունը ուղղահայաց է երկու զուգահեռ ուղիղներից մեկին, ապա այն ուղղահայաց է նաև մյուսին:
2. Նույն հարթությանը ուղղահայաց երկու ուղիղները զուգահեռ են:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009