14. Ապացույց հակասող ենթադրությամբ

\(a\) ուղիղը ուղղահայաց է $\mathrm{\alpha }$ հարթությանը և \(n\) ուղղին, որը ընկած չէ $\mathrm{\alpha }$ հարթության մեջ: 

 

Ապացուցիր, որ \(n\) ուղիղը զուգահեռ է $\mathrm{\alpha }$ հարթությանը:

 

 

             \(a\)                                                                                        \(n\)

 

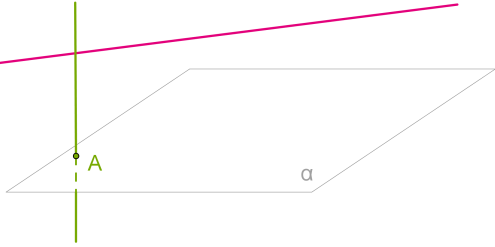
1. Եթե ուղիղը ընկած չէ հարթության մեջ, ապա այն կարող է կամ  լինել հարթությանը, կամ էլ՝ հարթությունը:

 

2. Ենթադրենք, թե \(n\) ուղիղը  չէ $\mathrm{\alpha }$ հարթությանը և  է այն:

 

3. Քանի որ \(a\) ուղիղը ուղղահայաց է $\mathrm{\alpha }$ հարթությանը, ապա այն  է այդ հարթության մեջ գտնվող ցանկացած ուղղին, մասնավորապես նաև այն ուղղին, որն անցնում է \(a\) և \(n\) ուղիղների և $\mathrm{\alpha }$ հարթության հատման կետերով:

 

4. Ստացանք իրավիճակ, երբ մի կետից \(a\) ուղղին տարված են երկու ուղիղներ:

 

5. Սա հակասություն է, որն ապացուցում է, որ \(n\) ուղիղը  է $\mathrm{\alpha }$ հարթությանը: