
















Երեք ուղղահայացների թեորեմը
Եթե հարթության մեջ թեքի հիմքով անցնող ուղիղը ուղղահայաց է թեքի պրոյեկցիային, ապա այն ուղղահայաց է նաև թեքին:
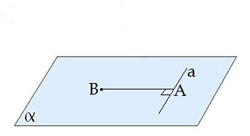 \(a\)\(AB\) | 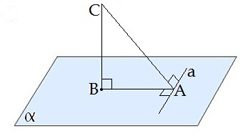 |
Ճիշտ է նաև հակադարձ թեորեմը:
Եթե հարթության մեջ գտնվող ուղիղը ուղղահայաց է թեքին, ապա այն ուղղահայաց է նաև նրա պրոյեկցիային այդ հարթության վրա:
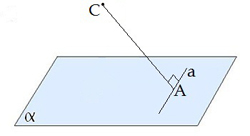 \(a\)\(AC\) |  |
Այսպիսով, ճիշտ է երկկողմանի թեորեմը:
Հարթության մեջ թեքի հիմքով անցնող ուղիղն ուղղահայաց է թեքին այն և միայն այն դեպքում, երբ այն ուղղահայաց է թեքի պրոյեկցիային այդ հարթության վրա:
Նկատենք, որ թեորեմում խոսվում է երեք ուղղահայացների՝ \(AC\), \(AB\) և \(CB\) ուղիղների մասին: Այդ պատճառով այն անվանում են թեորեմ երեք ուղղահայացների մասին:
Դիցուք \(S\) կետից \(ABCD\) ուղղանկյան հարթությանը տարված է \(BS\) ուղղահայացը և \(SA\), \(SC\), \(SD\) թեքերը:
Նշենք \(S\) գագաթով բոլոր ուղղանկյուն եռանկյունները:
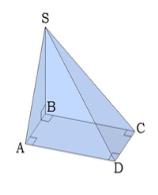 \(ABCD\)-ն ուղղանկյուն է, որի բոլոր անկյունները -ի են: 1. \(ASB\) նիստը ուղղանկյուն եռանկյուն է, 2. \(BSC\) նիստը ուղղանկյուն եռանկյուն է, քանի որ \(BS\)-ը ուղղահայաց է հիմքի հարթությանը: |
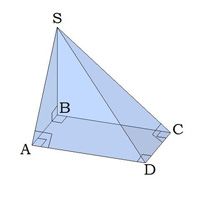 3. \(DSC\) նիստը ուղղանկյուն եռանկյուն է, ըստ երեք ուղղահայացների մասին թեորեմի՝ Հետևաբար, \(SCD =\) 4. \(ASD\) նիստը ուղղանկյուն եռանկյուն է, ըստ երեք ուղղահայացների մասին թեորեմի՝ Հետևաբար, \(SAD =\) Աղբյուրները Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009 |