
















Այն բուրգը, որի հիմքը կանոնավոր բազմանկյուն է, իսկ բուրգի գագաթի պրոյեկցիան հիմքի հարթության վրա հիմքի կենտրոնն է, կոչվում է կանոնավոր բուրգ:
Կարևոր է իմանալ կանոնավոր բուրգի հետևյալ երկու հատկությունները:
Հատկություն 1: Կանոնավոր բուրգի բոլոր կողմնային կողերը հավասար են, ընդ որում՝ դրանք հիմքի հարթության հետ կազմում են հավասար անկյուններ:
Հատկություն 2: Կանոնավոր բորգի կողմնային նիստերը հավասարասրուն և միմյանց հավասար եռանկյուններ են:
Կանոնավոր բուրգի կողմնային նիստի բարձրությունը կոչվում է հարթագիծ:
Կանոնավոր բուրգի բոլոր հարթագծերը հավասար են:
Դիտարկենք կանոնավոր բուրգի կարևոր մասնավոր դեպքերը՝
- կանոնավոր եռանկյուն բուրգ,
- կանոնավոր քառանկյուն բուրգ,
- կանոնավոր վեցանկյուն բուրգ:
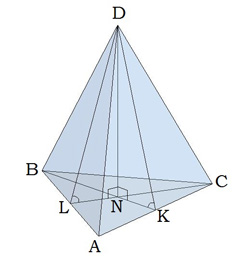
Կանոնավոր եռանկյուն բուրգ
Կանոնավոր եռանկյուն բուրգի հիմքը հավասարակողմ եռանկյուն է:
Բուրգի գագաթի պրոյեկցիան հիմքի եռանկյան միջնագծերի հատման կետն է:
Հիշիր՝
\(BN:NK = 2:1\)
\(KD\)-ն հարթագիծն է,
\(NKD\)-ն և \(NLD\)-ն հիմքին առընթեր երկնիստ անկյուններն են,
\(DCN\)-ն և \(DBN\)-ն հիմքի հարթության հետ կողմնային կողերի կազմած անկյուններն են:
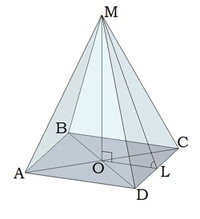
Կանոնավոր քառանկյուն բուրգ
Կանոնավոր քառանկյուն բուրգի հիմքը քառակուսի է:
Բուրգի գագաթի պրոյեկցիան հիմքի քառակուսու անկյունագծերի հատման կետն է:
\(ML\)-ը հարթագիծն է,
\(MLO\)-ն հիմքին առընթեր երկնիստ անկյունն է,
\(MCO\)-ն հիմքի հարթության հետ կողմնային կողի կազմած անկյունն է:
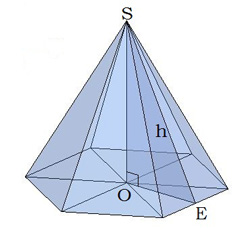
Կանոնավոր վեցանկյուն բուրգ
Կանոնավոր վեցանկյուն բուրգի հիմքը կանոնավոր վեցանկյուն է:
Բուրգի գագաթի պրոյեկցիան հիմքի վեցանկյան անկյունագծերի հատման կետն է:
\(SE = h\)-ը հարթագիծն է, \(OES\)-ը հիմքին առընթեր երկնիստ անկյունն է:
Կանոնավոր բուրգի կողմնային մակերևույթի մակերեսը հաշվում են հետևյալ երկու բանաձևերի միջոցով՝
,
որտեղ \(P\)-ն հիմքի պարագիծն է, \(h\)-ը հարթագիծը, -ն՝ հիմքին առընթեր երկնիստ անկյունը:
Կանոնավոր բուրգի կողմնային մակերևույթի մակերեսը հավասար է հիմքի պարագծի և բուրգի հարթագծի արտադրյալի կեսին:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009