Հատած բուրգ — դաս։ Երկրաչափություն, 10-րդ դասարան.

Հատած բուրգ կոչվում է բուրգի այն մասը, որը գտնվում է բուրգի հիմքի և հիմքին զուգահեռ հարթության միջև:

Հատած բուրգի կողմնային նիստերը սեղաններ են:

S_{լրիվ} = S_{1} + S_{2} + S_{կողմն}

Հատած բուրգի լրիվ մակերևույթի մակերեսը հավասար է երկու հիմքերի և կողմնային մակերևույթի մակերեսների գումարին:

Եթե հատած բուրգի հիմքերը $n$-անկյուն բազմանկյուն է, ապա այն անվանում են $n$-անկյուն հատած բուրգ:

$n$-անկյուն բուրգն ունի $n+2$ նիստ՝ $2$ հիմք, $n$ կողմնային նիստ:

$n$-անկյուն բուրգն ունի $2n$ գագաթ՝ $n$ գագաթ յուրաքանչյուր հիմքում:

$n$-անկյուն հատած բուրգն ունի $3n$ կող` $n$ կողմնային կող, և $n$ կող յուրաքանչյուր հիմքում:

$n$-անկյուն հատած բուրգն ունի $n·(n-3)$ անկյունագիծ:

Կանոնավոր բուրգի հիմքին զուգահեռ հարթության հատումով առաջացած հատած բուրգը կոչվում է կանոնավոր հատած բուրգ:


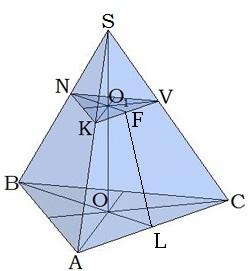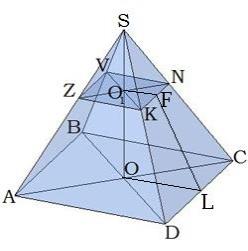$ABCKNV$-ն կանոնավոր եռանկյուն հատած բուրգ է: $ABC$-ն $KNV$-ն հատած բուրգի հիմքերն են, $O O_{1}$ -ը՝ բարձրությունը, $FL$-ը՝ հարթագիծը:	$ABCDZVNK$-ն կանոնավոր քառանկյուն հատած բուրգ է: $ABCD$-ն $ZVNK$-ն հատած բուրգի հիմքերն են, $O O_{1}$ -ը՝ բարձրությունը: $FL$-ը՝ հարթագիծը:

Կանոնավոր հատած բուրգի կողմնային մակերևույթի մակերեսը

S_{կողմն} = \frac{1}{2} (P_{1} + P_{2}) \cdot h

որտեղ

P_{1}, P_{2}

-ը հիմքերի պարագծերն են, $h$-ը՝ հարթագիծը:

Կանոնավոր հատած բուրգի կողմնային մակերևույթի մակերեսը հավասար է հիմքերի պարագծերի կիսագումարի և հարթագծի արտադրյալին:

Աղբյուրները

Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009

Սխա՞լ ես գտել

1. Հատած բուրգ