Բուրգի մակերևույթի մակերեսը — դաս։ Երկրաչափություն, 10-րդ դասարան.

Ցանկացած բուրգի լրիվ մակերևույթի մակերեսը հաշվում են հետևյալ բանաձևով՝

S_{լրիվ} = S_{հիմք} + S_{կողմն}

Բուրգի լրիվ մակերևույթի մակերեսը հավասար է նրա հիմքի և բոլոր կողմնային նիստերի մակերեսների գումարին:

Բուրգի կողմնային մակերևույթի մակերեսը

Որոշ դեպքերում բուրգի կողմնային մակերևույթի մակերեսը հնարավոր է լինում հաշվել հարմար բանաձևի միջոցով:

Արդեն գիտենք կանոնավոր բուրգի կողմնային մակերևույթի հաշվման բանաձևը:

Կանոնավոր բուրգի բոլոր կողմնային նիստերը հավասարասրուն եռանկյուններ են:

Քանի որ բոլոր այդ նիստերի հարթագծերը հավասար են, ապա գումարելով դրանց բոլորի մակերեսները, ստանում ենք՝

S_{կողմն} = \frac{P_{հիմք} \cdot h}{2}

որտեղ \(h\)-ը հարթագիծն է, իսկ

P_{հիմք}

-ը՝ հիմքի պարագիծը:

Ինչպես տեսանք, այս բանաձևի տեղի ունենալու համար կարևոր է, որ բուրգի բոլոր կողմնային նիստերի հարթագծերերը հավասար լինեն:

Հիշենք, որ այս պայմանը կատարվում է նաև այն դեպքում, երբ հավասար են բուրգի հիմքին առընթեր բոլոր երկնիստ անկյունները:

Եթե բուրգի կողմնային նիստերը հիմքի հարթության հետ կազմուն են հավասար երկնիստ անկյուններ, ապա բոլոր այդ նիստերի բարձրությունները հավասար են:

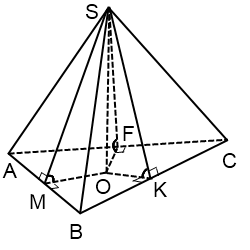
Հետևաբար, կանոնավոր բուրգի համար բերված կողմնային մակերևույթի մակերեսի բանաձևը տեղի ունի նաև այսպիսի բուրգերի դեպքում:

Եթե բուրգի կողմնային նիստերը հիմքի հարթության հետ կազմուն են հավասար երկնիստ անկյուններ, ապա բուրգի կողմնային մակերևույթի մակերեսը հավասար է նրա հիմքի պարագծի և հարթագծի արտադրյալի կեսին:

Կանոնավոր բուրգի լրիվ մակերևույթի մակերեսը

Մենք անդրադարձանք բուրգի կողմնային մակերևույթի մակերեսին:

Համաձայն

S_{լրիվ} = S_{հիմք} + S_{կողմն}

բանաձևի, բուրգի լրիվ մակերևույթի մակերեսը հաշվելու համար պետք է նաև կարողանալ հաշվել բուրգի հիմքի մակերեսը:

Բուրգի հիմքում բազմանկյուն է, որի մակերեսի հաշվման մասին խոսել ենք հարթաչափական պատկերներն ուսումնասիրելիս:

Սակայն այս դեպքում ևս կանոնավոր բուրգի համար հաջողվում է ստանալ հարմար բանաձև:

Մենք գիտենք կանոնավոր բազմանկյան մակերեսի հաշվման տարբեր եղանակներ:

Մասնավորապես՝

S_{հիմք} = \frac{P_{հիմք} \cdot r}{2}

որտեղ \(r\)-ը հիմքի ներգծյալ շրջանագծի շառավիղն է, իսկ

P_{հիմք}

-ը՝ հիմքի պարագիծը:

Գումարելով

S_{հիմք} = \frac{P_{հիմք} \cdot r}{2}

S_{կողմն} = \frac{P_{հիմք} \cdot h}{2}

բանաձևերը, ստանում ենք կանոնավոր բուրգի լրիվ մակերևույթի մակերեսի բանաձևը՝

S_{լրիվ} = \frac{P_{հիմք} \cdot (r + h)}{2}

Կանոնավոր բուրգի լրիվ մակերևույթի մակերեսը հավասար է նրա հիմքի ներգծյալ շրջանագծի ու հարթագծի գումարի և հիմքի պարագծի արտադրյալի կեսին:

Աղբյուրները

Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Բուրգի մակերևույթի մակերեսը

Տեսություն